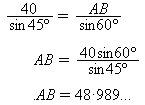Adding Vectors

From: M
Date: 20 October 1999

Subject: Adding Vectors

The streaks of rain of a railway carriage change from an
inclination of 15 degrees to the vertical when the train is at rest
to an inclination of 30 degrees on the opposite side of the vertical
when the train is travelling horizontally at 40km/hour.

Find the speed of the raindrops.

Maths Help suggests:

Vector diagram of velocities of train and raindrops

We are dealing with the vector quantities of velocity in this question.

A diagram of the vector triangle will help (see right).

Vector AB represents the velocity of the rain.
We don't know its magnitude (length) but
we know its angle is 15° to the vertical.
Vector BC represents the velocity of the train.
It has magnitude 40km/h and horizontal direction.
Vector AC represents the rain against the window of the moving train,
of unknown magnitude and at 30° to the vertical.

The speed of the raindrops is represented by the length AB.

Since ABC is not a right-angled triangle, we suggest the Sine Rule
to be the most direct method to find the required length:

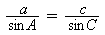
With a = 40, A = 45°, c = length AB, angle C = 60°.

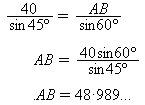
AC = 40sin 75/sin45 => AC = 54.6

So the speed of the rain is 49.0 km/h (3sf)

Return to contents list