Differentiation by First Principles

From: Martin Bland
Date: 28 August 1999

I have a question to differentiate y=x² by first principles.

The answer is 2x, isn't it?
But what does the by first principles bit mean?

The question says you should differentiate y = x² by first principles.

This means you are not allowed just to write down the answer using any
'short-cut' rules, but must use the 'official' method as follows:

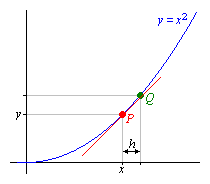
First, consider a sketch of the graph of y = x² (right).

You have to find an expression for , which represents
the gradient of the graph at the point P.

Point P has coordinates (x,x²) and
Q is a nearby point with coordinates (x + h,(x + h)²).

The line through P and Q has almost the correct gradient.
Its gradient is
(Increase in y)/(Increase in x)

So
gradient = (x+h)^2-x^2/h = 2x+h

Now this answer of 2x + h is almost the correct answer for .

As Q 'slides down' to get closer and closer to P:

We write:
dy/dx = lim(2x+h,h->0) = 2x

This is the answer you expected, but done without reference to any 'short cut' rules!