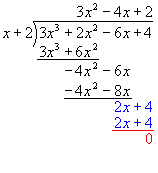Write the problem as shown on the right.
Note that the terms are written in descending powers of x.
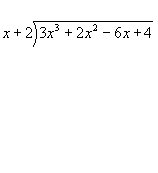
Always focus first on the leading terms.
Find how many times x goes into 3x3.
The result is 3x2.
Write the result in the x2 column on the solution line.
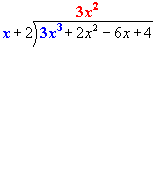
Now multiply the whole of x + 2 by 3x2.
The result is 3x3 + 6x2.
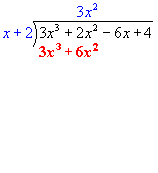
Subtract, giving a remainder of -4x2.
Bring down the -6x.
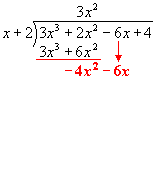
Now focus again on the leading terms.
Find how many times x goes into -4x2.
The result is -4x. Write this on the solution line.
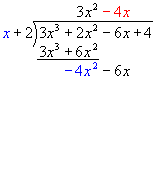
Multiply the whole of x + 2 by -4x.
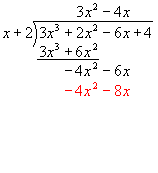
Subtract, giving a remainder of 2x.
Bring down the 4.
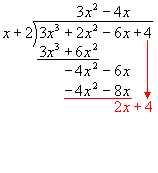
Find how many times x goes into 2x.
The result is 2. Write this on the solution line.
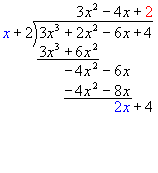
Multiply the whole of x + 2 by 2.
The result is 2x + 4.
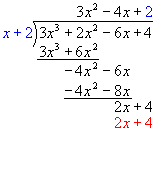
Subtract.
The remainder is zero.
This means that x + 2 is a factor of the original cubic.